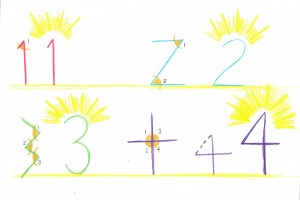Day 65
For one year, 365 days, this blog will address the Common Core Standards from the perspective of creating an alternate, ambient learning environment for math. Ambient is defined as “existing or present on all sides, an all-encompassing atmosphere.” And ambient music is defined as: “Quiet and relaxing with melodies that repeat many times.”
Why ambient? A math teaching style that’s whole and all encompassing, with themes that repeat many times through the years, is most likely to be effective and successful. Because the Common Core Grade 1 Math Standards address addition and subtraction exclusively, they will not appear here until math blocks 3 and 4: the 4 Processes. Math blocks 1 and 2 focus on meeting the numbers up close and personal, through stories, movement, art, and hands-on activities like making real numbers. (Note that Grade 1 math could be divided into three blocks of 20 days each: Number Forms/Real Numbers/4 Processes & Practice, or four blocks of 15 days each: Number Forms/Real Numbers/4 Processes/4 Processes Practice.)
There are many theories regarding the origins of the Arabic numerals. They are thought to have originated in India, so the term Arabic may be somewhat of a misnomer. Roman numerals were very slowly replaced by the Arabic, meeting with much resistance. Italy especially was a stronghold for the status quo, since the Roman numerals were considered holy and sanctioned (by the Catholic Church) while the Arabic were considered heathen symbols.
To elicit a meaningful connection with numbers and their interaction, it’s necessary to build the foundation of where the numbers’ forms came from. It’s always essential to pair the stages of child development with cultural development. Though it may be challenging for an adult to think of the numbers as foreign objects or pieces in an unknown puzzle, they do indeed appear that way to anyone who’s never seen them (i.e., a child).
In a lecture on reading and writing by master Waldorf teacher Eugene Schwartz, he points out this very element: that since the letters are foreign symbols to anyone who doesn’t yet know them, they need to be introduced both slowly and pictorially. Also that the straight line and curve element of form drawing can segue nicely into letter formation. The letter forms are then more familiar when brought through the story and drawn large on the page.
This thinking is transposed from letters to numbers, but can be a lot more explicit with the numbers, by introducing them through one of the many theories of how the Arabic numbers came to be. A simple story can be told as an introduction (similar to the story for the Roman numerals) before drawing the numbers as they evolved. The following is an excerpt from Math by Hand’s version of the Al-Khwarizmi theory.
“This theory is based on angles and a version of the abacus (a wooden frame with wires and beads, used for counting). Arabic mathematician Al-Khwarizmi (c. 778-850) invented this theory. Using the abacus notations, he developed the manuscript decimal system. He defined the numbers 1, 2, 3, and 4 based on additive angles. The forms of the numbers 5-10 were based on his knowledge of the abacus manuscript notations, a system using a special abacus with a base-5/10 like the human hands.
The angles for 1-4 are basic, as you see below. The numbers 5 and 10 are represented by circles symbolizing the closed hand, and 6, 7, 8, and 9 add or subtract angles. (You can find the whole set online). The numbers were modified over time and with use, as some elements were added or removed for clarity or convenience.”
Of course these abstract details would not be shared with the child(ren), but rather a colorful, simple story that conveys the idea would be told. Here is an excerpt from a story in the Grade 1 Daily Lesson Plans book, building on the idea of the abacus and counting beads.
“Naomi, a little shepherd girl, wondered if she could create some friendly counting symbols instead of using beads to count. Suddenly, as she was drawing in the damp sand with a finger, a wonderful idea came to her. What if little golden corners on the symbols showed how much each one was? There could be one corner for 1, two for 2, three for 3, and four for 4 . . .”
Tune in tomorrow for the exciting story of Zero! Remember that knowledge ensues in an environment dedicated to imaginative, creative knowing, where student and teacher alike surrender to the ensuing of that knowledge as a worthy goal.