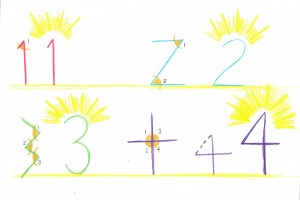
Day 65
For one year, 365 days, this blog will address the Common Core Standards from the perspective of creating an alternate, ambient learning environment for math. Ambient is defined as “existing or present on all sides, an all-encompassing atmosphere.” And ambient music is defined as: “Quiet and relaxing with melodies that repeat many times.”
Why ambient? A math teaching style that’s whole and all encompassing, with themes that repeat many times through the years, is most likely to be effective and successful. Because the Common Core Grade 1 Math Standards address addition and subtraction exclusively, they will not appear here until math blocks 3 and 4: the 4 Processes. Math blocks 1 and 2 focus on meeting the numbers up close and personal, through stories, movement, art, and hands-on activities like making real numbers. (Note that Grade 1 math could be divided into three blocks of 20 days each: Number Forms/Real Numbers/4 Processes & Practice, or four blocks of 15 days each: Number Forms/Real Numbers/4 Processes/4 Processes Practice.)
There are many theories regarding the origins of the Arabic numerals. They are thought to have originated in India, so the term Arabic may be somewhat of a misnomer. Roman numerals were very slowly replaced by the Arabic, meeting with much resistance. Italy especially was a stronghold for the status quo, since the Roman numerals were considered holy and sanctioned (by the Catholic Church) while the Arabic were considered heathen symbols.
To elicit a meaningful connection with numbers and their interaction, it’s necessary to build the foundation of where the numbers’ forms came from. It’s always essential to pair the stages of child development with cultural development. Though it may be challenging for an adult to think of the numbers as foreign objects or pieces in an unknown puzzle, they do indeed appear that way to anyone who’s never seen them (i.e., a child).
In a lecture on reading and writing by master Waldorf teacher Eugene Schwartz, he points out this very element: that since the letters are foreign symbols to anyone who doesn’t yet know them, they need to be introduced both slowly and pictorially. Also that the straight line and curve element of form drawing can segue nicely into letter formation. The letter forms are then more familiar when brought through the story and drawn large on the page.
This thinking is transposed from letters to numbers, but can be a lot more explicit with the numbers, by introducing them through one of the many theories of how the Arabic numbers came to be. A simple story can be told as an introduction (similar to the story for the Roman numerals) before drawing the numbers as they evolved. The following is an excerpt from Math by Hand’s version of the Al-Khwarizmi theory.
“This theory is based on angles and a version of the abacus (a wooden frame with wires and beads, used for counting). Arabic mathematician Al-Khwarizmi (c. 778-850) invented this theory. Using the abacus notations, he developed the manuscript decimal system. He defined the numbers 1, 2, 3, and 4 based on additive angles. The forms of the numbers 5-10 were based on his knowledge of the abacus manuscript notations, a system using a special abacus with a base-5/10 like the human hands.
The angles for 1-4 are basic, as you see below. The numbers 5 and 10 are represented by circles symbolizing the closed hand, and 6, 7, 8, and 9 add or subtract angles. (You can find the whole set online). The numbers were modified over time and with use, as some elements were added or removed for clarity or convenience.”
Of course these abstract details would not be shared with the child(ren), but rather a colorful, simple story that conveys the idea would be told. Here is an excerpt from a story in the Grade 1 Daily Lesson Plans book, building on the idea of the abacus and counting beads.
“Naomi, a little shepherd girl, wondered if she could create some friendly counting symbols instead of using beads to count. Suddenly, as she was drawing in the damp sand with a finger, a wonderful idea came to her. What if little golden corners on the symbols showed how much each one was? There could be one corner for 1, two for 2, three for 3, and four for 4 . . .”
Tune in tomorrow for the exciting story of Zero! Remember that knowledge ensues in an environment dedicated to imaginative, creative knowing, where student and teacher alike surrender to the ensuing of that knowledge as a worthy goal.
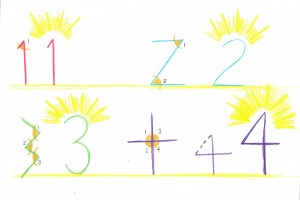
Tags:
Day 64
For one year, 365 days, this blog will address the Common Core Standards from the perspective of creating an alternate, ambient learning environment for math. Ambient is defined as “existing or present on all sides, an all-encompassing atmosphere.” And ambient music is defined as: “Quiet and relaxing with melodies that repeat many times.”
Why ambient? A math teaching style that’s whole and all encompassing, with themes that repeat many times through the years, is most likely to be effective and successful. Because the Common Core Grade 1 Math Standards address addition and subtraction exclusively, they will not appear here until math blocks 3 and 4: the 4 Processes. Math blocks 1 and 2 focus on meeting the numbers up close and personal, through stories, movement, art, and hands-on activities like making real numbers. (Note that Grade 1 math could be divided into three blocks of 20 days each: Number Forms/Real Numbers/4 Processes & Practice, or four blocks of 15 days each: Number Forms/Real Numbers/4 Processes/4 Processes Practice.)
The recommendation throughout the Kindergarten posts here was to compute using symbols rather than the Arabic numerals, since they are too abstract to use until they are properly introduced. After the Roman numerals are taught with a story and yesterday’s hand trace, the Arabic numerals can follow suit. There are many theories about the origins of the Arabic numerals, and it almost doesn’t matter which one is chosen, but it is necessary to place the Arabic numerals in some sort of context. Note that the concept of zero is essential to grasp for computation to take place, and it’s an especially difficult one to explain. Consider that it was only adopted in Europe in the ninth century, after a monumental struggle, especially with the Catholic church! As always, story and illustration are the vehicles of choice for optimal teaching and learning.
Math By Hand now has a Daily Lesson Plans supplemental book for Grades 1 and 2. The story of how the Roman numerals came to be is taken from the very end of the first math block, and could be told before doing yesterday’s hand trace drawing . . .
Roman Numerals
Once when the world was very young, the sun shone gold as it does today, but many things were very different. Straight brown sticks and small smooth stones were piled up at every door of every house, to be used for counting. You see, there were no numbers then, but so many things still needed to be counted! In order to count things, the small smooth stones or the straight sticks were gathered in groups to show how many.
One day a small boy used a stick to make marks in the soft, flat ground at his doorstep to show how many ears of corn he had picked that day. And those marks became the first written numbers. Then a little shepherd girl in the desert (where there were no trees, no branches, and no sticks) began counting on her fingers. And so it was for a long, long time.
Until, in a city of seven hills called Rome, written numerals were used. The Roman numerals looked like counting on your fingers: one finger (one straight line) was used for the number 1, two straight lines for the number 2, three straight lines for the number 3, but “V” was used for the number 5! Look at your hand. See if you can find the V for the number 5.
Tune in tomorrow for the story of the Arabic numerals’ beginnings, and how they first appeared. Remember that knowledge ensues in an environment dedicated to imaginative, creative knowing, where student and teacher alike surrender to the ensuing of that knowledge as a worthy goal. More Grade 1 numbers tomorrow!
Tags:
Day 63
For one year, 365 days, this blog will address the Common Core Standards from the perspective of creating an alternate, ambient learning environment for math. Ambient is defined as “existing or present on all sides, an all-encompassing atmosphere.” And ambient music is defined as: “Quiet and relaxing with melodies that repeat many times.”
Why ambient? A math teaching style that’s whole and all encompassing, with themes that repeat many times through the years, is most likely to be effective and successful. Because the Common Core Grade 1 Math Standards address addition and subtraction exclusively, they will not appear here until the Grade 1 math blocks 3 and 4: the 4 Processes. Math blocks 1 and 2 focus on meeting the numbers up close and personal through stories, movement, art, and hands-on activities like making real numbers. (Note that Grade 1 math could be divided into three blocks of 20 days each: Number Forms/Real Numbers/4 Processes & Practice, or four blocks of 15 days each: Number Forms/Real Numbers/4 Processes/4 Processes Practice.)
This will be a shorty blog, partially pre-empted by a fabulous concert, Wynton Marsalis and the Jazz at Lincoln Center Orchestra (not bad for our small town here in the N. Cali Sierra Foothills). Two of tonight’s selections were my faves. The first was “It’s Not Easy Being Green” and the second was the encore, Marsalis on trumpet accompanied only by bass, drums, and piano. The first debuted on Sesame Street, sung by Jim Henson as Kermit the Frog. Here are the lyrics:
It’s not that easy being green;
Having to spend each day the color of the leaves.
When I think it could be nicer being red, or yellow or gold-
or
something much more colorful like that.
It’s not easy being green.
It seems you blend in with so many other ordinary things.
And people tend to pass you over ’cause you’re not standing out like
flashy sparkles in the water-
or
stars in the sky.
But green’s the color of Spring.
And green can be cool and friendly-like.
And green can be big like an ocean, or
important like a mountain, or tall like a tree.
When green is all there is to be
It could make you wonder why, but why wonder?
Why Wonder, I am green and it’ll do fine, it’s beautiful!
And I think it’s what I want to be.
Originally sung by Jim Henson/Kermit the Frog
This resonated for me with a simpler, quieter time in education when Kindergarten was stories and naps, milk and cookies, and play, play, play. The grades were taught by real, live teachers loving to teach and loving their rooms full of kids. A time when the basics were enough, and testing was only little daily quizzes, plus teacher-made midterms and finals. And assessment was a handwritten blue report card, seen only by the teacher, child, and parent. Perhaps Ipads and apps might be the flashy sparkles on the water? And might I say that our education system may very well need to be made green again: slowed down and simplified.
Here’s the Roman numeral hand trace as promised yesterday. Have the child(ren) trace first the left, than both hands together, with a pencil. Note the “V” and “X” (5 and 10), and know that all the lively color isn’t just fancy frills. The child from 7 to 14 needs to be educated with heart and art, and the operative word here is “needs” because the heart connection is absolutely necessary for what’s being taught to be properly received. You will find that the rainbow is a recurring theme, an expression of the irrepressible joy that shines through when children are artfully taught. Knowledge ensues in an environment dedicated to imaginative, creative knowing, where student and teacher alike surrender to the ensuing of that knowledge as a worthy goal. More Grade 1 numbers tomorrow!

Tags:
Day 62
For one year, 365 days, this blog will address the Common Core Standards from the perspective of creating an alternate, ambient learning environment for math. Ambient is defined as “existing or present on all sides, an all-encompassing atmosphere.” And ambient music is defined as: “Quiet and relaxing with melodies that repeat many times.”
Why ambient? A math teaching style that’s whole and all encompassing, with themes that repeat many times through the years, is most likely to be effective and successful. Because the Common Core Grade 1 Math Standards address addition and subtraction exclusively, they will not appear here until the Grade 1 math blocks 3 and 4: the 4 processes. Math blocks 1 and 2 focus on meeting the numbers up close and personal through stories, movement, art, and hands-on activities like making real numbers.
If the numbers 1 to 12 are taught in the first math block, they can be spaced this way: a number story is told on Monday, after the form drawing main lesson. Three more number stories are told on Tuesday, Wednesday, and Thursday, and those stories are retold and illustrated the next day, so four numbers are covered each week. For a 20 day (or 4 week) block, the last week could focus on first the Roman and then the Arabic numerals.
The Waldorf curriculum follows child development as it parallels cultural development. The learning process then, begins with the beginning. Introducing the history and development of numbers through stories and pictures before using the numbers abstractly is therefore a sensible and wise approach. The Roman numerals are more concrete and direct than the Arabic, so that’s a good place to begin. It can be shown that they relate to counting on the fingers: l, ll, lll, and that the Roman numeral for 5 is derived from the “V” between the thumb and index finger, as the one for 10 is taken from the “X” formed by the two crossed thumbs.
It’s nice to do a hand tracing with the child(ren) to illustrate this and since a picture is always worth a thousand words, I will post the hand trace drawing in living color here tomorrow. Remember, knowledge ensues in an environment dedicated to imaginative, creative knowing, where student and teacher alike surrender to the ensuing of that knowledge as a worthy goal.
Tags:

Day 61
For one year, 365 days, this blog will address the Common Core Standards from the perspective of creating an alternate, ambient learning environment for math. Ambient is defined as “existing or present on all sides, an all-encompassing atmosphere.” And ambient music is defined as: “Quiet and relaxing with melodies that repeat many times.”
Why ambient? A math teaching style that’s whole and all encompassing, with themes that repeat many times through the years, is most likely to be effective and successful. Because the Common Core Math Standards for Grade 1 address addition and subtraction only, they will not appear here until the Grade 1 math blocks 3 and 4. Math blocks 1 and 2 focus on meeting the numbers up close and personal through stories, movement, art, and hands-on activities like making real numbers. Today’s post will be devoted to moving the numbers on a circle.
As shown in the illustrations below, the numbers and letters can be physically experienced, making them “bodily known” rather than memorized or understood only intellectually. Trace a large circle (at least 4 feet in diameter) on the floor indoors or outdoors on asphalt or sandy ground. Here’s an easy way to make a large circle: using a piece of twine or yarn that’s half the diameter of the finished circle (i.e. 2 feet for a 4 foot circle), tie one end to a pencil and the other to a piece of chunky chalk. Place the pencil and string in the center of the circle and have someone hold it there. Trace the circle with the chalk while holding the twine taut.
This could happen after the numbers or letters have been introduced through stories and illustrations. Have the child(ren) place beanbags (indicated by the red X’s) on the circle where the number or letter starts and stops, whether on the circle or not. Then have the child(ren) walk or run the number form. Note that the arrows show direction and starting points, and the dotted lines indicate “tip toe steps” where it’s necessary to go back to the top (or side) to continue the number or letter. This can help with correct formation and preventing reversals. PS, just noticed that the 1 and 7 are missing their ending beanbag red X’s. The perfect part of me wants to go back and redraw and rescan. But the sensible part wins tonight: the “PS” will do the trick . . .
Beyond practical purposes though, this sort of activity provides a context for learning and gives the child an edge, that of feeling ownership toward what’s being learned. Joy is such an integral part of wholesome teaching and learning, and this is truly a joyful process. No bored, sad faces or lack of energy here. Watch for smiles, laughter, and bounding through the forms with lively vigor (NOT rigor)! And remember always that knowledge ensues in an environment dedicated to imaginative, creative knowing, where student and teacher alike surrender to the ensuing of that knowledge as a worthy goal. More Grade 1 numbers tomorrow . . .


Tags:
Day 60
For one year, 365 days, this blog will address the Common Core Standards from the perspective of creating an alternate, ambient learning environment for math. Ambient is defined as “existing or present on all sides, an all-encompassing atmosphere.” And ambient music is defined as: “Quiet and relaxing with melodies that repeat many times.”
Why ambient? A math teaching style that’s whole and all encompassing, with themes that repeat many times through the years, is most likely to be effective and successful. Back to Kindergarten today, for a sad story. This from a Mom in Chicago who proctored one of her 6 year old daughter’s standardized tests, given in a computer lab with inadequate equipment. It seems stories like these are cropping up everywhere. All the trouble with the Common Core can perhaps help wake us up to the fact that education needs first and foremost to be age-appropriate and child-centered.
Knowledge ensues in an environment dedicated to imaginative, creative knowing, where student and teacher alike surrender to the ensuing of that knowledge as a worthy goal. Back to Grade 1 numbers tomorrow . . .
Here’s a story from Chicago by Claire Wapole, a mother who helped her six year old daughter’s class with standardized computerized testing, and the tears and frustration resulting from that experience. Here is an excerpt from Testing? Testing?:
I recently volunteered to be on the frontlines of testing. I offered to help during the MAP (Measures of Academic Progress) test administered to my daughter’s kindergarten class. For two days the teacher needed to be pulled out of the classroom along with all of the kids. They would be set up in a room with computers where the test would be given. Parents were needed to act more or less as proctors during the test, being on hand to assist with the equipment, then acting as runners to take the kids who had completed the test back to their classroom. In the classroom a paid for out of the school’s meager budget substitute teacher would be waiting to receive them. At no point during the MAP testing were the parents or the teacher permitted to help a kid arrive at an answer. They were there to help with the temperamental computers and to escort the kids back to their classrooms. Period.
Unless you have been around kindergarteners lately, it is easy to forget just how tiny they are. They are little itty-bitty people. They still have little teeny tiny teeth in their mouths. Many still have slight speeches issues, an ever-facing aural link to their toddler selves. After a bloodless injury like a bumped knee or pinch finger, they still wail pitifully for a band aid, still believing with all their heart that band aids make boo boos feel better. Kindergartners are indeed students, but awfully pint-sized students.
So on the day of this MAP test, all these little peanuts sit down in chairs, each in front of a computer. They have all been here the day before, day one was used to test their “reading” skills. I am there on day two, which is assessing math skills. No one’s feet touched the floor. Their hands are smaller than the mouses they hold. They are instructed to put on their headsets. The headsets are meant for adult sized people, not teeny people. I notice that for most kids, the headsets were way too big. If these kindergarteners had been built by Dr. Frankenstein the headsets would have hung down to the two bolts coming out of their necks. Few kids complained or sought help though. Maybe they had done so the day before? Most either let them rest below their ears or used one hand to hold an earpiece on one ear while their other hand held the mouse. Optimal listening conditions it was not. My daughter did say to me “See mom, they don’t fit. And when the person on the computer starts talking, I can’t hear what they are saying.” Well, then, that could sort of skew a result couldn’t it? “Deal with it as best as you can” I said. “Hold it on one ear and listen on that side.” Her eyes filled with tears. “I tried to do that yesterday,” she said. “I can’t really hear.” She turned back to her computer. Even five year olds are self conscious of crying in front of their peers.
I would imagine, that for many five year olds, this MAP test would be the first time in their lives that they could not talk through problem with an adult, or have an adult use different words that would help them better understand a problem. I understand that the testing field has to be equal, but I am here to tell you, it just feels wrong for a child so young not to be able to ask for clarification. Here is an example of what I mean: One question on the MAP test asked the kids to choose the picture that best represented something divided into three equal parts. “I don’t understand what divided means. What does that word mean?” a little girl asked me. “Ahh, I’m sorry. I can’t tell you.” I said. Her little face looked up at me confused and somewhat betrayed. “Why? Why can’t you tell me? Because you know I really don’t understand what divided is. I need your help.” “I’m sorry.” I said feeling like the slug adult I was “I can’t help you with that. Do the best you can.” I saw a couple of kids choosing the wrong answer to that problem and I wondered if those answers were being recorded as the students not being able to recognize three equal parts when they see it clearly drawn. I HOPE what was noted was that at age five they don’t understand the robust vocabulary word “divided” because that, in fact was “the problem”, not their ability to visually ascertain equality of shares.
Other hands were being raised asking for help. “This mouse doesn’t work. See I want to pick that answer,” a little boy said pointing to a spot on the far left hand corner of his screen. “But this mouse won’t go there. It’s broke.” I looked down at the mouse. The boy had moved it over to the left on the table, but his hand and the mouse had hit the keyboard, stopping the mouse from moving any further. “Here” I said. “When that happens you need to pick the mouse up, move it in the air over this way, set it back down, and move it on the table again.” I picked the mouse up, moved it to the right set it down, and showed him how he could then move the curser to the left once more. “But I don’t want to move it that way”. He said pointing to the right. “I want to move it this way,” he pointed to the left. “I know it seems weird.” I said. “But when the mouse won’t let you move it on the table you need to pick it up, fly it through the air and set it down again.” Is five too young to learn the concept of counter intuitiveness? Hey kid, slow is fast, less is more, you got to be cruel to be kind and you have to move the mouse to the right in order for you to then move it left. This “broken mouse” scenario played out several times, and remember, these kids had taken the test the day before, so I would imagine even more of them had this problem during the previous test.
Another hand goes up “Something happened” a little girl said. “I don’t know what this is,” She pointed at the screen. She had gotten herself into “preferences.” I took the mouse and said “Let’s see if I can get you out of here and back to your test.” I clicked onto the “close” button. Click. Click. Clickclickclickclickclickclickclick. It took a half dozen or so clicks before the window closed and the little test taker with the big bow in her hair was back to her assessment. This was played out again, and again and again, throughout the duration of the test. In a perfect world, where all the computers worked, testing conditions would be less frustrating. But it’s the real world, and a five year old could click on the wrong thing, and accidentally leave the test. Even when they do click on the button they want, the computers don’t always respond to their commands. I know it’s a computer or mouse glitch, but I can’t help but wonder how many of these kids think it’s their fault. I heard “I can’t do this” frequently. “Yes you can”. I said. “You are doing great. It’s the computer, not you.” The preferences or options screens were accidentally opened quite often. Other computer issues complicated the situation too. Some kids had to leave one computer and find another one, or switch out mouses. Computers fail, it’s a fact, but a lot of these little people felt the fault was theirs.
In the midst of all of this, I walked past my daughter. She looked up at me, her face red from crying, I could see that tears had been collecting at her collar “I just can’t do this,” she sobbed. The ill fitting headsets, the hard to hear instructions, the uncooperative mouse, the screen going to command modes, not being able to get clarification when she asked for it… her little psyche had reached it’s breaking point. It took just two days of standardized testing for her to doubt herself, quickly trading a love of learning for the shame of incompetence. Later on when I picked her up after her long seven-hour day, she whispered into my shoulder “I’m just not smart mom. Not like everyone else. I’m just no good at kindergarten, just no good at all.”
Tags:
Day 59
For one year, 365 days, this blog will address the Common Core Standards from the perspective of creating an alternate, ambient learning environment for math. Ambient is defined as “existing or present on all sides, an all-encompassing atmosphere.” And ambient music is defined as: “Quiet and relaxing with melodies that repeat many times.”
Why ambient? A math teaching style that’s whole and all encompassing, with themes that repeat many times through the years, is most likely to be effective and successful. Now it’s time to meet the numbers! Of course, by age 6-7 most children already know numbers and counting. But Grade 1 offers an opportunity to formally introduce them through content-rich lessons that are built on stories, pictures, and movement.
The Common Core Math Standards for Grade 1 rigorously plunge into abstract calculation in addition and subtraction, having laid the groundwork in Kindergarten and in some cases Pre-Kindergarten. Though a lot of the Common Core math early childhood curriculum tends to be healthily mixed with play, hands-on learning, and movement, much of the academic content remains too direct and thoroughly age-inappropriate. A five year old made to sit down and fill in workbook pages for hours on end is not fulfilling any good purpose, including and perhaps primarily, an academic one.
A truly healthy, holistic math curriculum however, following the solid pedagogical tenets of Piaget, Dewey, Steiner, and Montessori paces the immersion into math slowly, carefully, and broadly. Such is the Waldorf approach. So, after the form drawing block (with form drawing brought back every Monday, all year) the numbers from 1-12 are introduced through fairy tales. The essence of the number is conveyed through the story. A story about the sun or moon might be told for the number 1 as an example of singleness or oneness, while relating the number 1 to the uniqueness of each individual as well.
The week could be structured like this. A vigorous, lively 20 minutes or so of recitation, rhythmic movement, and singing first thing, every morning, followed by the 1 1/2 – 2 hour main lesson: Monday, form drawing, then the story for the number 1 is told. Tuesday, the story is retold by the child(ren), illustrated and captioned with the number 1 drawn large and carefully on the facing page, then the story for the number 2 is told. This rhythm continues until the number 12 is reached.
Each day is layered with alternating in and out breaths, beginning with the circle as an out-breath. The story and illustration, as in-breaths, are followed by a lively play break and nutritious snack. Skills practice could come next for 20 minutes or so, then lunch. And a wonderfully free afternoon of handwork, gardening, cooking, field trips, fun! This sort of alternating schedule really does mimic breathing, with quiet listening or working as breathing in, and playing or lively movement as breathing out.
Compare this to a full, 6 or 7 hour day of seat work, as so many Kindergarten children are enduring in the administration’s effort to cover all the ground required by the new standards. Let’s get back to basics! And get on track for slow learning, as a haven and respite from the hurried, harried pace endured by all these days. For knowledge ensues in an environment dedicated to imaginative, creative knowing, where student and teacher alike surrender to the ensuing of that knowledge as a worthy goal. See you tomorrow for more Grade 1 numbers . . .
Tags:
Day 58
For one year, 365 days, this blog will address the Common Core Standards from the perspective of creating an alternate, ambient learning environment for math. Ambient is defined as “existing or present on all sides, an all-encompassing atmosphere.” And ambient music is defined as: “Quiet and relaxing with melodies that repeat many times.”
Why ambient? A math teaching style that’s whole and all encompassing, with themes that repeat many times through the years, is most likely to be effective and successful. Today’s post will focus a bit more on block scheduling before proceeding with Grade 1 content. As a Waldorf class teacher I loved teaching in blocks, and it was so apparent that the children did too. Attempting to teach 3, 4, or 5 subjects in one day makes for a long day and can tend to be disjointed and scattered.
One of the best aspects of block scheduling is having the afternoons free. A very favorite teaching afternoon happened in my Grade 3 class and went like this: Since gardening was a main focus, we had been keeping a worm bin, maintained by lunch scraps! One of the Grade 3 jobs was to go to each of the classrooms with a bucket after lunch and collect everyone’s compost, which was then divided between the worm bin and our compost pile. At the end of the worm sojourn, I spread large sheets of white paper on the floor and placed the worm village on it. I had everyone gather round and each tally a group of worms to see how many we had grown! Squirmy, squealy fun was had by all, and the worms were then happily ensconced in our garden beds.
This is just one example of how the homeschool or classroom environment can “get real” and take a break from worksheets and testing. Maybe this activity could be matched with a Common Core standard, I hope so. But whether you are teaching with standards or without them, the block method is optimal for efficiency, teacher-student success, and all around good learning and play.
Here are some concrete advantages:
1) A “steeping” in each subject enhances interest and can foster greater retention: Devoting 2 hours each morning for 3-4 weeks to one subject helps to deepen the connection to it and reinforces what is learned each day.
2) Provides an antidote to the hurried and scattered nature of modern life, while also helping to address ADD or other attention challenges: Learning by the clock (scheduling different subjects each day to fit into individual time slots) tends to create a rushed and harried feeling. It can be beneficial for our children who so naturally seem to operate in a more “timeless” way, to be able to relax into each subject, taking more time with it. Children with ADD symptoms will benefit, since block scheduling is more grounded and slower paced.
3/ Allows a healthy “mix” of academics, arts, and recreation within the daily, weekly, and monthly schedules: If a concentrated block is set aside for more effective learning each day, it seems easier and more manageable to schedule other lessons and activities around it.
4) It’s easier for the parent/teacher to set up scheduling and lesson plans while making sure all bases are covered: Setting up a comprehensive plan at the beginning of the year seems to be a better organizational approach, and the concentrated blocks allow for more material to be covered in less overall time.
Knowledge ensues in an environment dedicated to imaginative, creative knowing, where student and teacher alike surrender to the ensuing of that knowledge as a worthy goal. See you tomorrow for more Grade 1 fun!
Tags:
Day 57
For one year, 365 days, this blog will address the Common Core Standards from the perspective of creating an alternate, ambient learning environment for math. Ambient is defined as “existing or present on all sides, an all-encompassing atmosphere.” And ambient music is defined as: “Quiet and relaxing with melodies that repeat many times.”
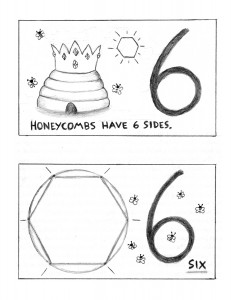
Why ambient? A math teaching style that’s whole and all encompassing, with themes that repeat many times through the years, is most likely to be effective and successful. For today’s post, a treat: sweeter than honey. One of my favorite fairy tales, The Queen Bee, can be told to introduce the letter B and the number 6. See below for the two drawings that illustrate the story, the number 6, and the hexagram.
Knowledge ensues in an environment dedicated to imaginative, creative knowing, where student and teacher alike surrender to the ensuing of that knowledge as a worthy goal. We’ll be getting to know the numbers 1-12, up close and personal, starting tomorrow . . .
The Queen Bee
The Brothers Grimm
Two kings’ sons once went out in search of adventures, and fell into a wild, disorderly way of living, so that they never came home again. The youngest, who was called Simpleton, set out to seek his brothers, but when at length he found them they mocked him for thinking that he with his simplicity could get through the world, when they two could not make their way, and yet were so much cleverer. They all three traveled away together, and came to an ant-hill. The two elder wanted to destroy it, to see the little ants creeping about in their terror, and carrying their eggs away, but Simpleton said, “Leave the creatures in peace, I will not allow you to disturb them.” Then they went onwards and came to a lake, on which a great number of ducks were swimming. The two brothers wanted to catch a couple and roast them, but Simpleton would not permit it, and said, “Leave the creatures in peace, I will not suffer you to kill them.” At length they came to a bee’s nest, in which there was so much honey that it ran out of the trunk of the tree where it was. The two wanted to make a fire beneath the tree, and suffocate the bees in order to take away the honey, but Simpleton again stopped them and said, “Leave the creatures in peace, I will not allow you to burn them.” At length the three brothers arrived at a castle where stone horses were standing in the stables, and no human being was to be seen, and they went through all the halls until, quite at the end, they came to a door in which were three locks. In the middle of the door, however, there was a little pane, through which they could see into the room. There they saw a little grey man, who was sitting at a table. They called him, once, twice, but he did not hear, at last they called him for the third time, when he got up, opened the locks, and came out. He said nothing, however, but conducted them to a handsomely spread table, and when they had eaten and drunk, he took each of them to a bedroom.
Next morning the little grey man came to the eldest, beckoned to him, and conducted him to a stone table, on which were inscribed three tasks, by the performance of which the castle could be delivered from enchantment. The first was that in the forest, beneath the moss, lay the princesses’ pearls, a thousand in number, which must be picked up, and if by sunset one single pearl was missing, he who had looked for them would be turned into stone. The eldest went thither, and sought the whole day, but when it came to an end, he had only found one hundred, and what was written on the table came true, and he was turned into stone. Next day, the second brother undertook the adventure, but it did not fare much better with him than with the eldest, he did not find more than two hundred pearls, and was changed to stone. At last it was Simpleton’s turn to seek in the moss, but it was so difficult for him to find the pearls, and he got on so slowly, that he seated himself on a stone, and wept. And while he was thus sitting, the king of the ants whose life he had once saved, came with five thousand ants, and before long the little creatures had got all the pearls together, and laid them in a heap. The second task, however, was to fetch out of the lake the key of the king’s daughters’ bed-chamber. When Simpleton came to the lake, the ducks which he had saved swam up to him, dived down, and brought the key out of the water. But the third task was the most difficult, from amongst the three sleeping daughters of the king was the youngest and dearest to be sought out. They, however, resembled each other exactly, and were only to be distinguished by their having eaten different sweetmeats before they fell asleep, the eldest a bit of sugar, the second a little syrup, and the youngest a spoonful of honey. Then the queen of the bees, whom simpleton had protected from the fire, came and tasted the lips of all three, and at last she remained sitting on the mouth which had eaten honey, and thus the king’s son recognized the right princess.
Then the enchantment was at an end, everything was delivered from sleep, and those who had been turned to stone received once more their natural forms. Simpleton married the youngest and sweetest princess, and after her father’s death became king, and his two brothers married the two other sisters. And all lived together happily and peacefully.
Tags:
Day 55
For one year, 365 days, this blog will address the Common Core Standards from the perspective of creating an alternate, ambient learning environment for math. Ambient is defined as “existing or present on all sides, an all-encompassing atmosphere.” And ambient music is defined as: “Quiet and relaxing with melodies that repeat many times.”
Why ambient? A math teaching style that’s whole and all encompassing, with themes that repeat many times through the years, is most likely to be effective and successful. Today’s post will focus on the Common Core Geometry Standard #3 which will appear in blue, followed by its ambient counterpart.
Geometry 1.G
Reason with shapes and their attributes.
Partition circles and rectangles into two and four equal shares, describe the shares using the words halves, fourths, and quarters, and use the phrases half of, fourth of, and quarter of, describe the whole as two of, or four of the shares. Understand for these examples that decomposing into more equal shares creates smaller shares.
The Waldorf method waits until Grade 4 to introduce fractions because the stages of child development determine the time frame of the curriculum. There are solid physiological reasons to wait until age 7 to begin formal teaching, and there are parallel reasons at every stage and age to introduce concepts at the optimal time. Every one of the child’s growth stages marks a significant step away from childhood. The Waldorf method recognizes and heeds these milestones as the drivers of what’s introduced when. For example, creation stories and housebuilding are told and taught in Grade 3 because at age 9, the leave-taking from the garden of childhood is especially intense. Creation stories address this leaving the garden as another step into the world, while supporting accompanying feelings of loss with the tools of living on the earth: gardening, housebuilding, and other useful crafts.
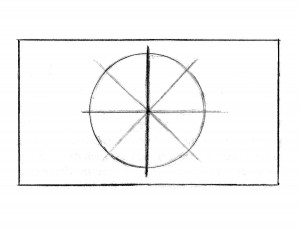
Fractions wait until Grade 4 because they echo the feelings of separation that manifest at that age. Everything in Grade 1 is steeped in the holistic. The circle is broken up into parts, but from a very different angle. When the numbers are introduced, a piece of fruit is cut up to show how 1 becomes 2, 2 becomes 4, and 4 becomes 8. The form drawing at the bottom of the page represents this concept. Wholeness is key now, and though many circles, squares, rectangles, triangles, hexagons, octagons, and more will be partitioned into two and four (and more) equal shares with form drawing, they are not equated with fraction terminology.
Faith and trust in the child, the teacher or parent, and the things of the world that can reveal themselves in due course and at just the right time is the golden rule. Because true knowledge ensues in an environment dedicated to imaginative, creative knowing, where student and teacher alike surrender to the ensuing of that knowledge as a worthy goal. As we leave geometry, please be assured that all the Common Core asks and so much more will be covered by the excellence that is form drawing. On to the numbers tomorrow!
Tags: