Who was Blaise Pascal? He left a lasting legacy of influence in many fields: theology, philosophy, literature, economics, social science, and mathematics, all in a short life of only 39 years.
Pascal’s mother died when he was only 3 years old, and his father, who was a judge and tax collector, homeschooled Blaise. His genius in mathematics first revealed itself when Pascal at only 13 years old discovered a mathematical error in the work of Rene Descarte.
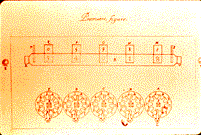
Three years later, Descarte declared that Pascal “knew more about mathematics than did all the ancients.” At 18, Blaise invented something that made his father’s staff of tax accountants’ workload easier. It was called the Pascaline, the first mechanical calculator. Many were against it however, because it was feared that since the Pascaline could do the work of six accountants, thousands would be unemployed because of it. Here’s a drawing:
Pascal originated the theory of probability, and in physics he discovered the foundation of modern hydraulics: Pascal’s Law. He also explained how air pressure works, in particular that the higher one goes above sea level the less air pressure there is.
Pascal readily admitted that technology and useful inventions, though beneficial to everyone, may very well convince the shallow-minded that science has a monopoly on truth, which he thought would be a grave error for the human race. Sadly, we see evidence of this same grave error everywhere today. Blaise Pascal said of mankind, “A drop of water can kill him; he is a feeble reed. But he is a thinking reed.”
He thought that humankind was both miserable and great, and that everything could not be explained through scientific formulae. That love, beauty, poetry and even good government are indefinable by science, as are spontaneous conduct, sympathy, friendship, or the love that fills the world.
Pascal famously said, “The heart has its reasons that the reason does not know.” Mathematics with heart, this is the formula for success in any math curriculum! With math lessons as well-rounded as Pascal’s views, your children will not only succeed at math, they will love it for life. And is this not after all the most desirable outcome?
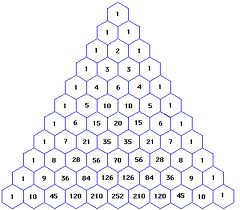
Pascal’s triangle is a wonderful example of his way of thinking. Its magnetic appeal prompts not only practical skill and knowledge, but fascination and interest as well. The triangle is simple in its concept and easy to construct, but contains many wonderful features. Addition skills are all that’s needed to construct it, and the premise is simple: each row builds upon the previous one. Here it is:
Here are some of its features; see if you and your students can discover others:
1) the outside rows are made up of 1’s
2) the second rows are the natural (counting) numbers
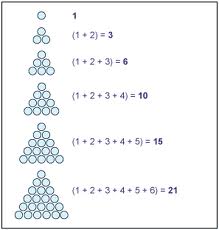
3) the third rows are the triangle numbers
Here are the triangle numbers (numbers that actually form triangles):
4) the third rows are also the square numbers, constructed like this:
1 + 3 = 4 (2 x 2)
3 + 6 = 9 (3 x 3)
6 + 10 = 16 (4 x 4)
10 + 15 = 25 (5 x 5)
15 + 21 = 36 (6 x 6)
21 + 28 = 49 (7 x 7)
28 + 36 = 64 (8 x 8)
36 + 45 = 81 (9 x 9)
5) the sum of each row, added across, doubles the one before it:
1 + 1 = 2
1 + 2 + 1 = 4
1 + 3 + 3 + 1 = 8
1 + 4 + 6 + 4 + 1 = 16
1 + 5 + 10 + 10 + 5 + 1 = 32
1 + 6 + 15 + 20 + 15 + 6 + 1 = 64
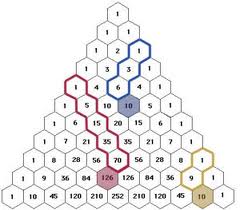
And last but not least, the hockey stick pattern! This means that a sharp turn to the left or right will result in the sum of all the numbers in the diagonal row before the turn. Here’s an example:
Have fun with Pascal’s triangle by having your students copy it onto a very large piece of paper. You’ll need to have scrap paper on hand to calculate the rows. And finally, have your students color the odd and even numbers with contrasting colors, and you will see triangles within triangles, like this: